CARL.BELLE

Home » Articles » QSharp » Contact

Pauli-X Gate

QSharp

On this page:

The Pauli-X Gate

The Pauli-X gate acts on a single qubit. It maps |0› to |1› and |1› to |0›. The Pauli-X gate is represented by the following matrix:

The Pauli-X matrix

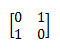
//	One-line notation
{{0, 1}, {1, 0}}

//	Expanded notation
{
{0, 1},
{1, 0}
}

Manipulation of a register takes the form of matrix algebra. In order for the mathematics to take place, matricies of appropriate size must be constructed. This can be a tedious and time consuming process.

Thankfully, there is an easier way to compute these outcomes, as will be demonstrated.

If you are unfamiliar with either tensor products or matrix multiplication, then I would suggest revising those topics first, otherwise a lot of this will look like magic.

Syntax

The Quantum Console syntax for this operation is:

X(n);

Where n specifies the number (or index) of the qubit we wish to manipulate.

* Note that this index is 0 based, not 1 based as represented in most examples.

1 Qubit Register

Performing this calculation on a single qubit is fairly straight forward, as the rules for matrix multiplication (number of columns from matrix A must match the number of rows from matrix B) are satisfied.

In other words, the number of columns in the Pauli-X matrix match the number of rows in the state vector.

Matrix mathematics

{
{0, 1},
{1, 0}
}

*
 
{
{A|0›},
{B|1›}
}

=
 Show intermediate working 
{
{B|1›},
{A|0›}
}

Performing the operation in Quantum Console

//	Qubits
(A|0› + B|1›)

//	Computational Basis States - Input
A|0› + B|1›

//	Quantum Console syntax
//	Apply X to qubit 0
X(0);

//	Computational Basis States - Ouput
B|0› + A|1›

2 Qubit Register

Performing this calculation becomes a little bit trickier, as our state vector is now larger (2n, n = 2) at 4 rows.

Consequently, as the state vector now has 4 rows, so an X gate cannot be applied to it, as the number of columns from matrix A (2) does not match the number of rows from matrix B (4).

To work around this, it is necessary to tensor an I (identity) matrix for each other qubit in order to construct the matrix of the appropriate size.

In this example, the X gate is applied to the qubit in position 1, and as the identity matrices are inferred, the operation could be written as:

IX

If the X gate was to be applied to the qubit in position 0, and as the identity matrices are inferred, the operation could be written as:

XI

Matrix mathematics

First, tensor the gate with an identity matrix:

{
{0, 1},
{1, 0}
}

(x)
 
{
{1, 0},
{0, 1}
}

=
 
{
{0, 0, 1, 0},
{0, 0, 0, 1},
{1, 0, 0, 0},
{0, 1, 0, 0}
}

This 'steps up' the X gate to be appropriately sized for the state vector.

Now the result can be applied to the state vector:

{
{0, 0, 1, 0},
{0, 0, 0, 1},
{1, 0, 0, 0},
{0, 1, 0, 0}
}

*
 
{
{AC|00›},
{AD|01›},
{BC|10›},
{BD|11›}
}

=
 Show intermediate working 
{
{BC|00›},
{BD|01›},
{AC|10›},
{AD|11›}
}

Performing the operation in Quantum Console

//	Qubits
(A|0› + B|1›) (x) (C|0› + D|1›)

//	Computational Basis States - Input
AC|00› + AD|01› + BC|10› + BD|11›

//	Quantum Console syntax
//	Apply X to qubit 1
X(1);

//	Computational Basis States - Ouput
AD|00› + AC|01› + BD|10› + BC|11›

3 Qubit Register

This time, the state vector is larger again (2n, n = 3), at 8 rows, and due to this an X gate cannot be applied as the number of columns from matrix A (2) does not match the number of rows from matrix B (8).

To work around this, as before, tensor an I (identity) matrix for each qubit involved that is not being manipulated in order to construct the matrix of the appropriate size.

In this example, the X gate is applied to the qubit in position 1, and as the identity matrices are inferred, the operation could be written as:

IXI

If the X gate was to be applied to the qubit in position 0, and as the identity matrices are inferred, the operation could be written as:

XII

Matrix mathematics

Tensor the gate with an identity.

Tensor products are produced by applying the left matrix to the right. So in this instance, the I is applied to the X first, then IX to I.

I (step 1: tensor) X (step 2: tensor) I

{
{1, 0},
{0, 1}
}

(x)
 
{
{0, 1},
{1, 0}
}

=
 
{
{0, 1, 0, 0},
{1, 0, 0, 0},
{0, 0, 0, 1},
{0, 0, 1, 0}
}

Tensor the product with another identity:

{
{0, 1, 0, 0},
{1, 0, 0, 0},
{0, 0, 0, 1},
{0, 0, 1, 0}
}

(x)
 
{
{1, 0},
{0, 1}
}

=
 
{
{0, 1, 0, 0, 0, 0, 0, 0},
{1, 0, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 1, 0, 0, 0, 0},
{0, 0, 1, 0, 0, 0, 0, 0}
{0, 0, 0, 0, 0, 1, 0, 0},
{0, 0, 0, 0, 1, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 1},
{0, 0, 0, 0, 0, 0, 1, 0}
}

The matrix is now the correct size to be applied to the state vector:

{
{0, 0, 1, 0, 0, 0, 0, 0},
{0, 0, 0, 1, 0, 0, 0, 0},
{1, 0, 0, 0, 0, 0, 0, 0},
{0, 1, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 1, 0},
{0, 0, 0, 0, 0, 0, 0, 1},
{0, 0, 0, 0, 1, 0, 0, 0},
{0, 0, 0, 0, 0, 1, 0, 0}
}

*
 
{
{ACE|000›},
{ACF|001›},
{ADE|010›},
{ADF|011›},
{BCE|100›},
{BCF|101›},
{BDE|110›},
{BDF|111›}
}

=
 Show intermediate working 
{
{ADE|010›},
{ADF|011›},
{ACE|000›},
{ACF|001›},
{BDE|110›},
{BDF|111›}
{BCE|100›},
{BCF|101›},
}

Performing the operation in Quantum Console

//	Qubits
(A|0› + B|1›) (x) (C|0› + D|1›) (x) (E|0› + F|1›)

//	Computational Basis States - Input
ACE|000› + ACF|001› + ADE|010› + ADF|011› + BCE|100› + BCF|101› + BDE|110› + BDF|111›

//	Quantum Console syntax
//	Apply X to qubit 1
X(1);

//	Computational Basis States - Ouput
ADE|000› + ADF|001› + ACE|010› + ACF|011› + BDE|100› + BDF|101› + BCE|110› + BCF|111›

n Qubit Register

As you can see from the previous examples, performing manual matrix arthimetic for each step becomes tedious and time consuming, however it is important to acknowledge that this process takes place in the first instance.

Thankfully, there is a much simpler way of working out these operations as we shall discover for an n qubit register.

Suppose an X gate is to be applied to qubit 1 in a register, as with the previous examples.

For a 2 qubit system, apply the X logic to the each bit indicated in the operation. X(1) for example, applies an X gate to every bit in position 1.

//	State vector
|ψ› = (AC|00› + AD|01› + BC|10› + BD|11›)

//	1 bit positions bolded - these are the bits that will be affected by the X operation
(AC|00› + AD|01› + BC|10› + BD|11›)

//	Apply the X to every bit that occupies the 1 position
X(1);

//	Intermediate working, to be rearranged
(AC|01› + AD|00› + BC|11› + BD|10›)

//	State vector - compare this to the matrix calculations above
|ψ› = (AD|00› + AC|01› + BD|10› + BC|11›)

Using the same methodology on a larger system reduces the amount of manual work. For a 3 qubit register:

//	State vector
|ψ› = (ACE|000› + ACF|001› + ADE|010› + ADF|011› + BCE|100› + BCF|101› + BDE|110› + BDF|111›)

//	1 bit positions bolded
(ACE|000› + ACF|001› + ADE|010› + ADF|011› + BCE|100› + BCF|101› + BDE|110› + BDF|111›)

//	Apply the X to every bit that occupies the 1 position
X(1);

//	Intermediate working, to be rearranged
(ACE|010› + ACF|011› + ADE|000› + ADF|001› + BCE|110› + BCF|111› + BDE|100› + BDF|101›)

//	State vector - compare this to the matrix calculations above
|ψ› = (ADE|000› + ADF|001› + ACE|010› + ACF|011› + BDE|100› + BDF|101› + BCE|110› + BCF|111›)

The Column Method

You might find that using the column method is easier and faster - it took a while for me to develop, but now I find it easier to use than other methods.

To use the column method:

  1. Write the state vector vertically down the page
  2. Write an index over each bit column
  3. Write the gate over the bit to be operated on
  4. Now, work out the result of the operation, one element at a time, and write these into a new column

Applying the column method to the 3 qubit example from above:

//	X(1);
//	Apply the X gate, one element at a time

 X
012

000  010	//	Remember the X gate flips the associated bit
001  011
010  000
011  001
100  110
101  111
110  100
111  101

Now, all that is left is to take the values from the left column and plug them into the right column:

     X
    012

ACE|000  ADE|010
ACF|001  ADF|011
ADE|010  ACE|000
ADF|011  ACF|001
BCE|100  BDE|110
BCF|101  BDF|111
BDE|110  BCE|100
BDF|111  BCF|101

And finally adjust the state vector (using the binary index) to match the new order:

ADE|000
ADF|001
ACE|010
ACF|011
BDE|100
BDF|101
BCE|110
BCF|111

The manipulation of the state vector is now complete.


 

Copyright © 2025 carlbelle.com